GATE 2001
Question 1 |
Consider the following statements:
- S1: The sum of two singular n × n matrices may be non-singular
S2: The sum of two n × n non-singular matrices may be singular.
Which of the following statements is correct?
S1 and S2 are both true | |
S1 is true, S2 is false | |
S1 is false, S2 is true | |
S1 and S2 are both false |

Question 2 |
Consider the following relations:
- R1(a,b) iff (a+b) is even over the set of integers
R2(a,b) iff (a+b) is odd over the set of integers
R3(a,b) iff a.b > 0 over the set of non-zero rational numbers
R4(a,b) iff |a-b| <= 2 over the set of natural numbers
Which of the following statements is correct?
R1 and R2 are equivalence relations, R3 and R4 are not | |
R1 and R3 are equivalence relations, R2 and R4 are not | |
R1 and R4 are equivalence relations, R2 and R3 are not | |
R1, R2, R3 and R4 are all equivalence relations |
a+a = 2a
The set (a,a) is reflexive.
The set representation (a,a), (b,b) is also Symmetric.
The set representation is Transitive.
So, this is Equivalence.
R2:
a+a ≠ 2a
The (a,a) is non-reflexive.
R3:
a⋅a>0 → Reflexive
a⋅b>0 and b⋅a>0 → Symmetric
a⋅b>0, b⋅c>0 then c⋅a>0 → Transitive
The relation R3 is equivalence relation.
R4:
|a - a| ≤ 2, which is not possible, not Reflexive.
R1 & R3 are equivalence, R2 & R4 are not.
Question 3 |
Consider two well-formed formulas in prepositional logic
F1: P ⇒ ¬P F2: (P⇒¬P)∨(¬P⇒P)
Which of the following statements is correct?
F1 is satisfiable, F2 is valid | |
F1 unsatisfiable, F2 is satisfiable | |
F1 is unsatisfiable, F2 is valid | |
F1 and F2 are both satisfiable |

F1 is satisfiable; F2 is valid.
Question 4 |
Consider the following two statements:
- S1: {02n|n≥1|} is a regular language
S2: {0m1n0m+n|m≥1 and n≥1|} is a regular language
Which of the following statements is correct?
Only S1 is correct | |
Only S2 is correct | |
Both S1 and S2 are correct | |
None of S1 and S2 is correct |
For S2, DFA is not possible which is not regular.
Question 5 |
Which of the following statements is true?
If a language is context free it can always be accepted by a deterministic push-down automaton | |
The union of two context free languages is context free | |
The intersection of two context free languages is context free | |
The complement of a context free language is context free |
Question 6 |
Given an arbitrary non-deterministic finite automaton (NFA) with N states, the maximum number of states in an equivalent minimized DFA is at least
N2 | |
2N | |
2N | |
N! |
If NFA have two states {1}{2} = 2
Then DFA may contain {ϕ}{1}{2}{1,2} = 4 = 22 = 2N
Question 7 |
More than one word is put in one cache block to
exploit the temporal locality of reference in a program | |
exploit the spatial locality of reference in a program | |
reduce the miss penalty | |
none of the above |
The temporal locality refers to reuse of data elements with a smaller regular intervals.
Question 8 |
Which of the following statements is false?
Virtual memory implements the translation of a program’s address space into physical memory address space | |
Virtual memory allows each program to exceed the size of the primary memory | |
Virtual memory increases the degree of multiprogramming | |
Virtual memory reduces the context switching overhead |
Question 9 |
A low memory can be connected to 8085 by using
INTER | |
 | |
HOLD | |
READY |
Question 10 |
Suppose a processor does not have any stack pointer register. Which of the following statements is true?
It cannot have subroutine call instruction | |
It can have subroutine call instruction, but no nested subroutine calls | |
Nested subroutine calls are possible, but interrupts are not | |
All sequences of subroutine calls and also interrupts are possible |
Question 11 |
Given the following Karnaugh map, which one of the following represents the minimal Sum-Of-Products of the map?

xy+y'z | |
wx'y'+xy+xz | |
w'x+y'z+xy | |
xz+y |
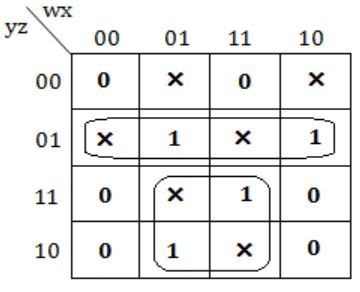
⇒ y'z + xy
Question 12 |
A processor needs software interrupt to
test the interrupt system of the processor | |
implement co-routines | |
obtain system services which need execution of privileged instructions | |
return from subroutine |
Question 13 |
A CPU has two modes-privileged and non-privileged. In order to change the mode from privileged to non-privileged
a hardware interrupt is needed | |
a software interrupt is needed | |
a privileged instruction (which does not generate an interrupt) is needed | |
a non-privileged instruction (which does not generate an interrupt is needed |
Question 14 |
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?
O(n) | |
O(n log n) | |
O(n2) | |
O(n!) |
Question 15 |
Consider any array representation of an n element binary heap where the elements are stored from index 1 to index n of the array. For the element stored at index i of the array (i≤n), the index of the parent is
i-1 | |
⌊i/2⌋ | |
⌈i/2⌉ | |
(i+1)/2 |
Left Child is at index: 2i
Right child is at index: 2*i+1
Question 16 |
Let f(n) = n2logn and g(n) = n(logn)10 be two positive functions of n. Which of the following statements is correct?
f(n) = O(g(n) and g(n) ≠ O(f(n)) | |
g(n) = O(f(n) and f(n) ≠ O(g(n)) | |
f(n) ≠ O(g(n)) and g(n) ≠ O(f(n)) | |
f(n) = O(g(n)) and g(n) = O(f(n)) |
Cancel nlogn from f(n), g(n)
f(n) = n; g(n) = (logn)9
n is too large than (logn)9
So f(n)! = O(g(n)) and g(n) = O(f(n))
Question 17 |
The process of assigning load addresses to the various parts of the program and adjusting the code and date in the program to reflect the assigned addresses is called
Assembly | |
Parsing | |
Relocation | |
Symbol resolution |
