GATE 2005
Question 1 |
What does the following C-statement declare?
int ( * f) (int * ) ;
A function that takes an integer pointer as argument and returns an integer. | |
A function that takes an integer as argument and returns an integer pointer. | |
A pointer to a function that takes an integer pointer as argument and returns an integer. | |
A function that takes an integer pointer as argument and returns a function pointer. |
→ A pointer to a function which takes integer as a pointer and return an integer value.
Question 2 |
An Abstract Data Type (ADT) is:
Same as an abstract class | |
A data type that cannot be instantiated
| |
A data type type for which only the operations defined on it can be used, but none else | |
All of the above |
Question 3 |
A common property of logic programming languages and functional languages is:
both are procedural languages | |
both are based on λ-calculus | |
both are declarative | |
both use Horn-clauses |
Question 4 |
Which one of the following are essential features of an object-oriented programming language?
- (i) Abstraction and encapsulation
(ii) Strictly-typedness
(iii) Type-safe property coupled with sub-type rule
(iv) Polymorphism in the presence of inheritance
(i) and (ii) only | |
(i) and (iv) only | |
(i), (ii) and (iv) only | |
(i), (iii) and (iv) only |
Question 5 |
A program P reads in 500 integers in the range [0, 100] representing the scores of 500 students. It then prints the frequency of each score above 50. What would be the best way for P to store the frequencies?
An array of 50 numbers | |
An array of 100 numbers | |
An array of 500 numbers | |
A dynamically allocated array of 550 numbers |
→ Then using array of 50 numbers is the best way to store the frequencies.
Question 6 |
An undirected graph C has n nodes. Its adjacency matrix is given by an n × n square matrix whose (i) diagonal elements are 0's and (ii) non-diagonal elements are l's. Which one of the following is TRUE?
Graph G has no minimum spanning tree (MST)
| |
Graph G has a unique MST of cost n-1 | |
Graph G has multiple distinct MSTs, each of cost n-1 | |
Graph G has multiple spanning trees of different costs |
Since the weights of every edge is 1 so there are different MST's are possible with same cost, i.e., (n-1).
Question 7 |
The time complexity of computing the transitive closure of a binary relation on a set of n elements is known to be:
O(n) | |
O(n log n) | |
O(n3/2) | |
O(n3) |
For example, if X is a set of airports and x R y means "there is a direct flight from airport x to airport y" (for x and y in X), then the transitive closure of R on X is the relation R+ such that x R+ y means "it is possible to fly from x to y in one or more flights". Informally, the transitive closure gives you the set of all places you can get to from any starting place.
To find the transitive closure of given relation, we can represent the given relation by the graph such that if x R y then there should be directed edge between x and y in a graph. For this graph, we have to apply modified Floyd_Warshall Algorithm to find the transitive closure of the graph.
The time complexity of this algorithm is O(V3) where V is the number of vertices in the given graph. You can take here V as the number of elements is set i.e., N. Therefore time complexity for the given question is O(n3).
Question 8 |
Let A, B and C be non-empty sets and let X = (A - B) - C and Y = (A - C) - (B - C). Which one of the following is TRUE?
X = Y | |
X ⊂ Y | |
Y ⊂ X | |
None of these |
B = {1, 3, 4, 5}
C = {2, 4, 5, 6}
X = (A - B) - C
X = {2, 6} - {2, 4, 5, 6}
= ∅
Y = (A - C) - (B - C)
= {1, 3} - { 1, 3}
= ∅
X = Y

X = (A - B) - C
= (1, 5) - (5, 7, 4, 3)
= (1)
Y = (A - C) - (B - C)
= (1, 4) - (2, 4)
= (1)
X = Y
Question 9 |
The following is the Hasse diagram of the poset [{a,b,c,d,e},<]
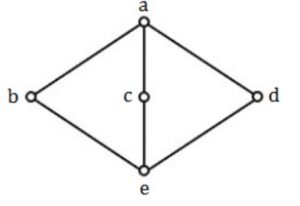
The poset is
not a lattice | |
a lattice but not a distributive lattice | |
a distributive lattice but not a Boolean algebra | |
a Boolean algebra |
But it is not distributed because for some element there are more than one complement. Moreover if it is not distributive then it can't be boolean.
Question 10 |
Let G be a simple connected planar graph with 13 vertices and 19 edges. Then, the number of faces in the planar embedding of the graph is:
6 | |
8 | |
9 | |
13 |
F = E - V + 2 [From Euler's formula i.e., F + V - E = 2]
F = 19 - 13 +2
F = 8
Question 11 |
Let G be a simple graph with 20 vertices and 100 edges. The size of the minimum vertex cover of G is 8. Then, the size of the maximum independent set of G is
12 | |
8 | |
Less than 8 | |
More than 12
|
Edges = 100
Minimum cover of vertex G is = 8
Maximum Independent set of G = No. of vertices - Minimum cover of vertex G
= 20 - 8
= 12
Question 12 |
Let f(x) be the continuous probability density function of a random variable X. The probability that a < X ≤ b, is:
f(b - a)
| |
f(b) - f(a) | |
 | |
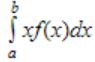 |
Then the probablity be area of the corresponding curve i.e.,

Question 13 |
The set {1, 2, 4, 7, 8, 11, 13, 14} is a group under multiplication modulo 15. The inverses of 4 and 7 are respectively:
3 and 13 | |
2 and 11 | |
4 and 13 | |
8 and 14 |
Inverse of 4 = m; Inverse of 7 = n
(4×m)%15=1; (7*n)%15=1
Option A: m=3 n=13
12%15≠1 (✖️) 91%15=1 (✔️)
Option B: m=2 n=11
8%15≠1 (✖️) 11%15≠1 (✖️)
Option C: m=4 n=13
16%15=1(✔️) 91%15=1 (✔️)
Option D: m=8 n=14
120%15≠1(✖️) 98%15≠1(✖️)
Question 14 |
The grammar A → AA | (A) | ε is not suitable for predictive-parsing because the grammar is:
ambiguous | |
left-recursive | |
right-recursive | |
an operator-grammar |
It have A → AA has left recursion.
Question 15 |
Consider the following circuit.
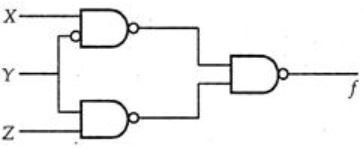
Which one of the following is TRUE?
f is independent of X
| |
f is independent of Y | |
f is independent of Z | |
None of X, Y, Z is redundant |
= ((X’+Y) YZ)’
= (X’YZ + YZ)’
= ((X’+1) YZ)’
= (YZ)’
Question 16 |
The range of integers that can be represented by an n bit 2's complement number system is:
- 2n-1 to (2n-1 - 1) | |
- (2n-1 - 1) to (2n-1 - 1) | |
- 2n-1 to 2n-1 | |
- (2n-1 + 1) to (2n-1 - 1) |
The smallest (negative) n bit number is 100..0 (i.e., 1 followed by n-1 zeros) which is equal to - 2n-1.
1000...00
0111...11 <- 1’s complement
1000..00 <- 2’s complement
= - 2n-1
Question 17 |
The hexadecimal representation of 6578 is
1AF | |
D78 | |
D71 | |
32F |
Make 3 zeros on the left side so that the number of bits is multiple of 4.
= (0001 1010 1111)2
= (1 A F)16
Question 18 |
The switching expression corresponding to f(A, B, C, D) = Σ (1, 4, 5, 9, 11, 12) is:
BC'D' + A'C'D + AB'D | |
ABC' + ACD + B'C'D | |
ACD' + A'BC' + AC'D' | |
A'BD + ACD' + BCD' |

f(A,B,C,D) = A'C'D + BC'D' + AB'D
Question 19 |
Which one of the following is true for a CPU having a single interrupt request line and a single interrupt grant line?
Neither vectored interrupt nor multiple interrupting devices are possible.
| |
Vectored interrupts are not possible but multiple interrupting devices are possible.
| |
Vectored interrupts and multiple interrupting devices are both possible.
| |
Vectored interrupt is possible but multiple interrupting devices are not possible. |
Also for vectored Interrupts it is always possible if we implement in daisy chain mechanism.
Question 20 |
Normally user programs are prevented from handling I/O directly by I/O instructions in them. For CPUs having explicit I/O instructions, such I/O protection is ensured by having the I/O instructions privileged. In a CPU with memory mapped I/O, there is no explicit I/O instruction. Which one of the following is true for a CPU with memory mapped I/O?
I/O protection is ensured by operating system routine(s)
| |
I/O protection is ensured by a hardware trap | |
I/O protection is ensured during system configuration
| |
I/O protection is not possible |
Question 21 |
What is the swap space in the disk used for?
Saving temporary html pages
| |
Saving process data
| |
Storing the super-block | |
Storing device drivers
|
→ The interchange of data between a virtual memory and a real memory is called as swapping and space on a disk as 'swap space'.
→ Swap space in the disk can be used for saving process data.
Question 22 |
Increasing the RAM of a computer typically improves performance because:
Virtual memory increases | |
Larger RAMs are faster | |
Fewer page faults occur | |
Fewer segmentation faults occur |
→ Such as if RAM size increases, then no. of page entries increases, then no. of page faults decreases.
