GATE 2008
Question 1 |
1 | |
-1 | |
∞ | |
-∞ |
Question 2 |
If P, Q, R are subsets of the universal set U, then (P∩Q∩R) ∪ (Pc∩Q∩R) ∪ Qc ∪ Rc is
Qc ∪ Rc | |
P ∪ Qc ∪ Rc | |
Pc ∪ Qc ∪ Rc | |
U |
(P∩Q∩R)∪(Pc∩Q∩R)∪Qc∪Rc
It can be written as the p.q.r + p'.q.r +q' + r'
=> (p+p').q.r + q' + r'
=> q.r + (q'+r')
=> q.r + q' + r' = 1 i.e., U
Question 3 |
The following system of equations
-
x1 + x2 + 2x3 = 1
x1 + 2x2 + 3x3 = 2
x1 + 4x2 + ax3 = 4
has a unique solution. The only possible value(s) for a is/are
0 | |
either 0 or 1 | |
one of 0, 1 or -1 | |
any real number |

When a-5 = 0, then rank(A) = rank[A|B]<3,
So infinite number of solutions.
But, it is given that the given system has unique solution i.e., rank(A) = rank[A|B] = 3 will be retain only if a-5 ≠ 0.
Question 4 |
In the IEEE floating point representation, the hexadecimal value 0×00000000 corresponds to
the normalized value 2 - 127 | |
the normalized value 2 - 126 | |
the normalized value + 0 | |
the special value + 0 |

Question 5 |
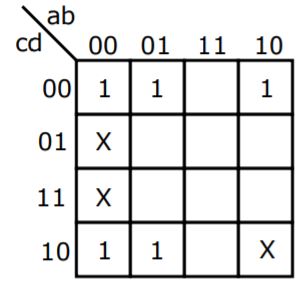
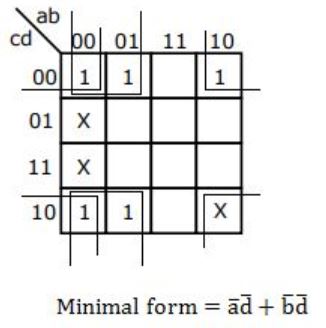
In the Karnaugh map shown below, X denotes a don’t care term. What is the minimal form of the function represented by the Karnaugh map?
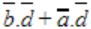 | |
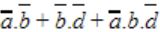 | |
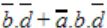 | |
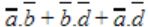 |
Question 6 |
Let r denote number system radix. The only value(s) of r that satisfy the equation is/are
decimal 10 | |
decimal 11 | |
decimal 10 and 11 | |
any value > 2 |
(r2 + 2r + 1)1/2 = r + 1
(r + 1)2 * 1/2 = r + 1
r + 1 = r + 1 Any value of r will satisfy the above equation. But the radix should be greater than 2 because the 121 has 2. So r > 2 is correct.
Question 7 |
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity
θ(n) | |
θ(m) | |
θ(m+n) | |
θ(mn) |
Suppose if we are using Adjacency matrix means it takes θ(n2).
Question 8 |
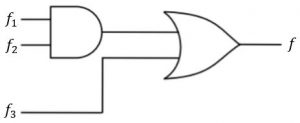
Given f1, f3 and f in canonical sum of products form (in decimal) for the circuit
- f1 = Σm(4,5,6,7,8)
f3 = Σm(1,6,15)
f = Σm(1,6,8,15)
then f2 is
Σm(4,6) | |
Σm(4,8) | |
Σm(6,8) | |
Σm(4,6,8) |
f1*f2 is intersection of minterms of f1 and f2
f = (f1*f2) + f3 is union of minterms of (f1*f2) and f3
Σm(1,6,8,15) = Σm(4,5,6,7,8) * f2 + Σm(1,6,15)
Options A, B and D have minterm m4 which result in Σm(1,4,6,15), Σm(1,4,6,8, 15) and Σm(1,4,6,8, 15)respectively and they are not equal to f.
Option C : If f2 = Σm(6,8)
RHS: Σm(4,5,6,7,8) * Σm(6,8) + Σm(1,6,15)
= Σm(6,8) + Σm(1,6,15)
= Σm(1,6,8,15)
= f = LHS
Question 9 |
Which of the following is true for the language {ap|p is a prime} ?
It is not accepted by a Turing Machine | |
It is regular but not context-free
| |
It is context-free but not regular | |
It is neither regular nor context-free, but accepted by a Turing machine |
Question 10 |
Which of the following are decidable?
-
I. Whether the intersection of two regular languages is infinite
II. Whether a given context-free language is regular
III. Whether two push-down automata accept the same language
IV. Whether a given grammar is context-free
I and II | |
I and IV | |
II and III | |
II and IV |
Statement IV is also decidable, we need to check that whether the given grammar satisfies the CFG rule (TYPE 2 grammar productions).
But statements II and III are undecidable, as there doesn’t exist any algorithm to check whether a given context-free language is regular and whether two push-down automata accept the same language.
Question 11 |
Which of the following describes a handle (as applicable to LR-parsing) appropriately?
It is the position in a sentential form where the next shift or reduce operation will occur.
| |
It is non-terminal whose production will be used for reduction in the next step. | |
It is a production that may be used for reduction in a future step along with a position in the sentential form where the next shift or reduce operation will occur.
| |
It is the production p that will be used for reduction in the next step along with a position in the sentential form where the right hand side of the production may be found.
|
Question 12 |
Some code optimizations are carried out on the intermediate code because
They enhance the portability of the compiler to other target processors | |
Program analysis is more accurate on intermediate code than on machine code
| |
The information from dataflow analysis cannot otherwise be used for optimization | |
The information from the front end cannot otherwise be used for optimization |
Question 13 |
If L and are recursively enumerable, then L is
regular | |
context-free | |
context-sensitive | |
recursive |
If
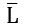 are recursively enumerable, then it implies that there exist a Turing Machine (lets say M2) which always HALT for the strings which is NOT in L(as L is complement of
are recursively enumerable, then it implies that there exist a Turing Machine (lets say M2) which always HALT for the strings which is NOT in L(as L is complement of 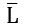 Since we can combine both Turing machines (M1 and M2) and obtain a new Turing Machine (say M3) which always HALT for the strings if it is in L and also if it is not in L. This implies that L must be recursive.
Since we can combine both Turing machines (M1 and M2) and obtain a new Turing Machine (say M3) which always HALT for the strings if it is in L and also if it is not in L. This implies that L must be recursive.
Question 14 |
What is the maximum size of data that the application layer can pass on to the TCP layer below?
Any size | |
216 bytes-size of TCP header | |
216 bytes | |
1500 bytes |
Transport Layer - 65515 byte
Network layer - 65535 byte
Data link layer - 1500 byte
Question 15 |
Which of the following tuple relational calculus expression(s) is/are equivalent to ∀t ∈ r(P(t))?
- I. ¬∃t ∈ r(P(t))
II. ∃t ∉ r(P(t))
III. ¬∃t ∈ r(¬P(t))
IV. ∃t ∉ r(¬P(t))
I only | |
II only | |
III only | |
III and IV only |
∀xP(x) ≡ ∼∃x(∼P(x))
∼∀x(∼P(x)) ≡ ∃x(P(x))
Given: ∀t ∈ r(P(t))------ (1)
As per Demorgan law
(1) ⇒ ∼∃t ∈ r(∼P(t))
which is option (III).
Question 16 |
A clustering index is defined on the fields which are of type
non-key and ordering | |
non-key and non-ordering | |
key and ordering
| |
key and non-ordering
|
Question 17 |
Which of the following system calls results in the sending of SYN packets?
socket | |
bind | |
listen | |
connect |
1) The client requests a connection by sending a SYN (synchronize) message to the server.
2) The server acknowledges this request by sending SYN-ACK back to the client.
3) The client responds with an ACK, and the connection is established.
Question 18 |
Which combination of the integer variables x, y and z makes the variable a get the value 4 in the following expression?
a = (x > y) ? ((x > z) ? x : z) : ((y > z) ? y : z)
x = 3, y = 4, z = 2 | |
x = 6, y = 5, z = 3 | |
x = 6, y = 3, z = 5 | |
x = 5, y = 4, z = 5 |
→ We can directly eliminate the options B & C, because none of the variable can assign a value 4.
→ Given explanation is
a = (x>y)?((x>z)?x:z):((y>z)?y:z)
Option A:
x=3; y=4; z=2
a=(3>4)? ⇒ No
Then evaluate second expression ⇒ (4>2)?Yes
⇒a=y
a=4 (True)
Option D:
x=5; y=4; z=5
a=(5>4) ⇒ Yes
Then evaluate first expression ⇒ (5>5)? No
⇒ a=z ⇒ a=5 (Not true)
⇒ Answer is Option A.
Question 19 |
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
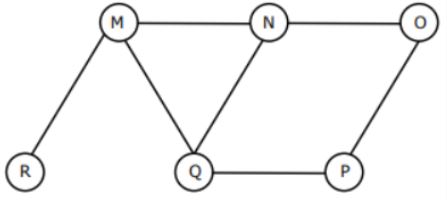
MNOPQR | |
NQMPOR | |
QMNPRO | |
QMNPOR |
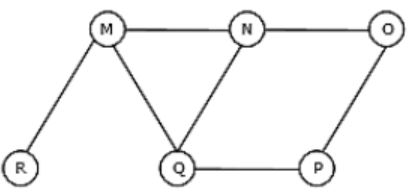
Option C: QMNPRO
→ Queue starts with Q then neighbours of Q is MNP and it is matching with the given string .
→ Now , Next node to be considered is M . Neighbours of M are N, Q and R , but N and Q are already in Queue. So, R is matching with one given string
→ Now, next node to be considered is N. Neighbours of N are M, Q and O, but M and Q are already in Queue. So, O is matching with a given string.
Hence , Option C is Correct.
Similarly, check for option (D).
Question 20 |
The data blocks of a very large file in the Unix file system are allocated using
contiguous allocation | |
linked allocation | |
indexed allocation | |
an extension of indexed allocation |
Question 21 |
The minimum number of equal length subintervals needed to approximate to an accuracy of atleast
using the trapezoidal rule is
1000e | |
1000 | |
100e | |
100 |