GATE 2011
Question 1 |
The simplified SOP (sum of product) form of the boolean expression
![]()
 | |
 | |
 | |
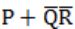 |
Question 2 |
The minimum number of D flip-flops needed to design a mod-258 counter is
9 | |
8 | |
512 | |
258 |
The max Mod values is 2n.
So 2n ≥ 258 ⇒ n = 9
Question 3 |
Which one of the following circuits is NOT equivalent to a 2-input XNOR (exclusive NOR) gate?
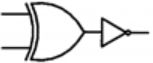 | |
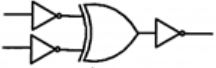 | |
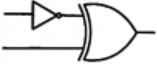 | |
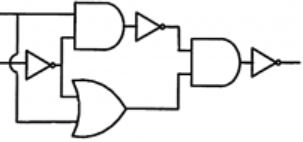 |
Question 4 |
A thread is usually defined as a "light weight process" because an operating system (OS) maintains smaller data structures for a thread than for a process. In relation to this, which of the following is TRUE?
On per-thread basis, the OS maintains only CPU register state | |
The OS does not maintain a separate stack for each thread | |
On per-thread basis, the OS does not maintain virtual memory state | |
On per thread basis, the OS maintains only scheduling and accounting information |
B) False, OS do maintain a separate stack for each thread.
C) True
D) False
Question 5 |
K4 and Q3 are graphs with the following structures.
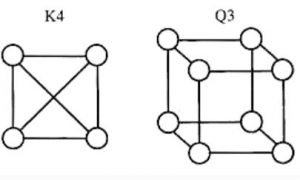
Which one of the following statement is TRUE in relation to these graphs?
K4 is planar while Q3 is not | |
Both K4 and Q3 are planar | |
Q3 is planar while K4 is not | |
Neither K4 not Q3 is planar |
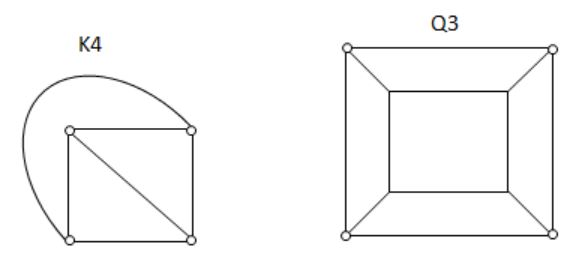
Both the above graphs are planar.
Question 6 |
If the difference between the expectation of the square of a random variable (E[X2]) and the square of the expectation of the random variable (E[X])2 is denoted by R, then
R = 0 | |
R < 0 | |
R ≥ 0 | |
R > 0 |
So the answer will be R≥0.
Question 7 |
The lexical analysis for a modern computer language such as Java needs the power of which one of the following machine models in a necessary and sufficient sense?
Finite state automata | |
Deterministic pushdown automata | |
Non-Deterministic pushdown automata | |
Turing machine |
Question 8 |
Let the page fault service time to 10 ms in a computer with average memory access time being 20 ns. If one page fault is generated for every 106 memory accesses, what is the effective access time for the memory?
21 ns | |
30 ns | |
23 ns | |
35 ns |
EA = p × page fault service time + (1 – p) × Memory access time
= 1/106×10×10
Question 9 |
Consider a hypothetical processor with an instruction of type LW R1, 20 (R2), which during execution reads a 32-bit word from memory and stores it in a 32-bit register R1. The effective address of the memory location is obtained by the addition of constant 20 and the contents of register R2. Which of the following best reflects the addressing mode implemented by this instruction for the operand memory?
Immediate Addressing | |
Register Addressing | |
Register Indirect Scaled Addressing | |
Base Indexed Addressing |
Question 10 |
What does the following fragment of C-program print?
char c[] = "GATE2011";
char *p =c;
printf("%s", p + p[3] - p[1]) ;
GATE2011 | |
E2011 | |
2011 | |
011 |
p[3] - p[1] = 4, and p+4 will be pointing to the fifth position in the array 'c'. So printf starts printing from 2 and prints 2011.
Question 11 |
A max-heap is a heap where the value of each parent is greater than or equal to the value of its children. Which of the following is a max-heap?
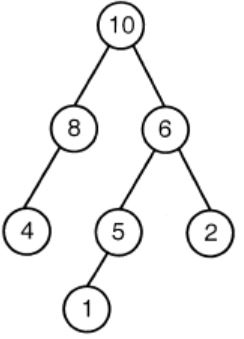 | |
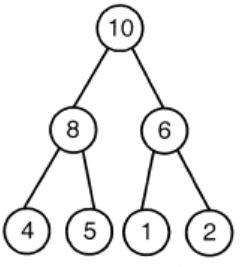 | |
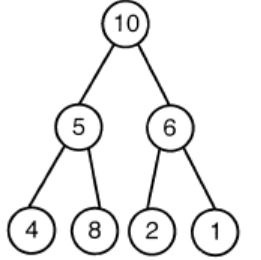 | |
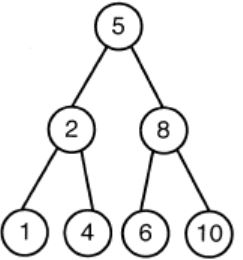 |
Option A: It violates the property of complete binary tree.
Option C: 8 is greater than 5. The root value is always greater than his children. So, the above tree is violating the property of max heap.
Option D: 10 is greater than 8. The root value is always greater than his children. So, the above tree is violating the property of max heap.
Question 12 |
An algorithm to find the length of the longest monotonically increasing sequence of numbers in an array A[0:n-1] is given below. Let Li denote the length of the longest monotonically increasing sequence starting at index i in the array
Initialize Ln-1=1. For all i such that 0≤i≤n-2
Finally the length of the longest monotonically increasing sequence is Max(L0, L1, ..., Ln-1).
Which of the following statements is TRUE?
The algorithm uses dynamic programming paradigm | |
The algorithm has a linear complexity and uses branch and bound paradigm | |
The algorithm has a non-linear polynomial complexity and uses branch and bound paradigm | |
The algorithm uses divide and conquer paradigm |
2. Dynamic programming is a technique used to avoid computing multiple time the same sub-problem in a recursive algorithm.
Note: It is neither backtracking nor branch and bound because we are not branching anywhere in the solution space. The algorithm is not divide and conquer as we are not dividing the problem and then merging the solution
Question 13 |
Let P be a regular language and Q be a context-free language such that Q ⊆ P. (For example, let P be the language represented by the regular expression p*q* and Q be [pnqn | n ∈ N]). Then which of the following is ALWAYS regular?
P ∩ Q | |
P – Q | |
Σ* – P | |
Σ* – Q |
since regular languages are closed under complementation.
Question 14 |
In a compiler, keywords of a language are recognized during
parsing of the program | |
the code generation | |
the lexical analysis of the program | |
dataflow analysis |
Question 15 |
A layer-4 firewall (a device that can look at all protocol headers up to the transport layer) CANNOT
block entire HTTP traffic during 9:00PM and 5:00AM | |
block all ICMP traffic | |
stop incoming traffic from a specific IP address but allow outgoing traffic to the same IP address | |
block TCP traffic from a specific user on a multi-user system during 9:00PM and 5:00AM |
(B) Possible because it is network layer protocol.
(C) Possible because SP address is present in Network layer.
(D) Not possible, because to block specific user, we need user id which is present in Application layer.
Question 16 |
If two fair coins are flipped and at least one of the outcomes is known to be a head, what is the probability that both outcomes are heads?
1/3 | |
1/4 | |
1/2 | |
2/3 |
Required probability = 1/3
