GATE 2017 [Set-1]
Question 1 |
I. p ⇒ q
II. q ⇒ p
III. (¬q) ∨ p
IV. (¬p) ∨ q
I only | |
I and IV only | |
II only | |
II and III only |
Construct Truth tables:
~p ⇒ ~q

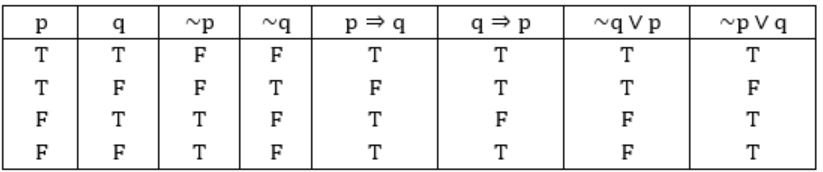
II, III are equivalent to (~p) ⇒ (~q)
Method 2:
(I) p⇒q ≡ ~p∨q
(II) q⇒p ≡ ~q∨p
(III) (~q) ∨ p ≡ ~q∨p
(IV) (~p) ∨ p ≡ ~p∨q
Also, from question:
(~p) ⇒ (~q)
≡ p∨~q
So, (II) & (III) are equivalent to the statement given in question.
Question 2 |
I. ∃y(∃xR(x,y))
II. ∃y(∀xR(x,y))
III. ∀y(∃xR(x,y))
IV. ¬∃x(∀y¬R(x,y))
IV only | |
I and IV only | |
II only | |
II and III only |
F: ∀x(∃yR(x,y)) (given)
: For all girls there exist a boyfriend
(x for girls and y for boys)
I: ∃y(∃xR(x,y))
: There exist some boys who have girlfriends.
(Subset of statement F, so True)
II: ∃y(∀xR(x,y))
: There exists some boys for which all the girls are girlfriend. (False)
III: ∀y(∃xR(x,y))
: For all boys exists a girlfriend. (False)
IV: ~∃x(∀y~R(x,y))
= ∀x(~∀y~R(x,y))
= ∀x(∃yR(x,y)) (∵ ~∀y=∃y, ~∃x=∀x)
(True)
Question 3 |
Let c1, cn be scalars not all zero. Such that the following expression holds:
where ai is column vectors in Rn. Consider the set of linear equations.
Ax = B.where A = [a1.......an] and ![]()
Then, Set of equations has
a unique solution at x = Jn where Jn denotes a n-dimensional vector of all 1 | |
no solution | |
infinitely many solutions | |
finitely many solutions |
AX = B
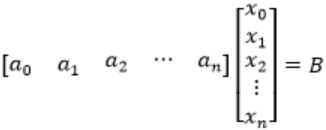
As given that
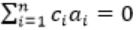 and c1&cn ≠ 0
and c1&cn ≠ 0 means c0a0 + c1a1 + ...cnan = 0, represents that a0, a1... an are linearly dependent.
So rank of 'A' = 0, (so if ‘B’ rank is = 0 infinite solution, ‘B’ rank>0 no solution) ⇾(1)
Another condition given here is, 'Σai = b',
so for c1c2...cn = {1,1,...1} set, it is having value 'b',
so there exists a solution if AX = b →(2)
From (1)&(2), we can conclude that AX = B has infinitely many solutions.
Question 4 |
Consider the following functions from positives integers to real numbers
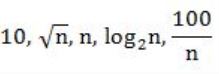
The CORRECT arrangement of the above functions in increasing order of asymptotic complexity is:
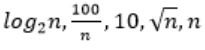 | |
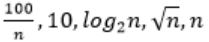 | |
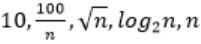 | |
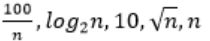 |
Step-1: Take n=2048 or 211 (Always take n is very big number)
Step-2: Divide functions into 2 ways
1. Polynomial functions
2. Exponential functions
Step-3: The above functions are belongs to polynomial. So, simply substitute the value of n,
First compare with constant values.
→ 100 / 2048 = 0.048828125
→ 10 > 100/ 2048
→ log2 2048 =11
→ √n = 45.25483399593904156165403917471
→ n = 2048
So, Option B is correct
Question 5 |
Consider the following table
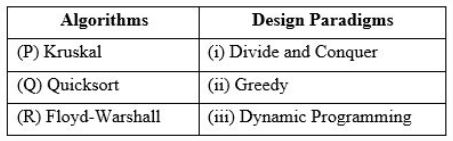
Match the algorithm to design paradigms they are based on:
(P)↔(ii), Q↔(iii), (R)↔(i) | |
(P)↔(iii), Q↔(i), (R)↔(ii) | |
(P)↔(ii), Q↔(i), (R)↔(iii) | |
(P)↔(i), Q↔(ii), (R)↔(iii) |
(Q) QuickSort is a Divide and Conquer algorithm.
(R) Floyd Warshall Algorithm is for solving the All Pairs Shortest Path problem using Dynamic Programming.
Some important points regarding Greedy Vs Dynamic Programming
Greedy: →
It always gives polynomial time complexity
→ It is not an optimal
→ It always selects only either minimum or maximum among all possibilities
→ Ex: Dijkstra’s algorithm for SSSP, Optimal Merge Pattern, Huffman coding, Fractional knapsack problem, etc..,
Dynamic Programming:
→ It gives either polynomial or exponential time complexity.
→ It gives always an optimal result.
→ It checks all possibilities of a problem.
→ Ex: Longest Common sequence, Matrix chain Multiplication, Travelling sales Problem, etc.
Question 6 |
Let T be a binary search tree with 15 nodes. The minimum and maximum possible heights of T are:
Note: The height of a tree with a single node is 0.4 and 15 respectively | |
3 and 14 respectively | |
4 and 14 respectively | |
3 and 15 respectively |
The height of a tree with single node is 0.
Minimum possible height is when it is a complete binary tree.
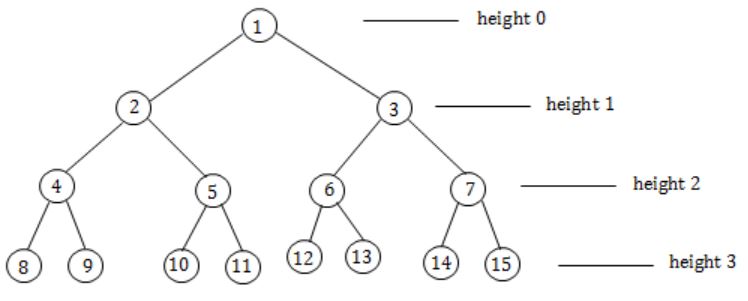
Maximum possible height is when it is a skewed tree left/right.
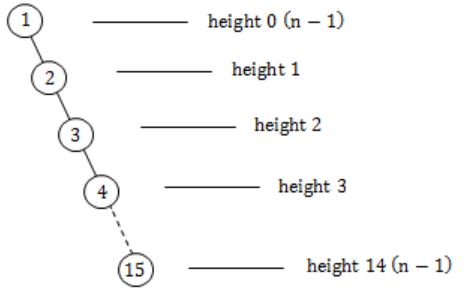
So the minimum and maximum possible heights of T are: 3 and 14 respectively.
Question 7 |
The n-bit fixed-point representation of an unsigned real number X uses f bits for the fraction part. Let i = n-f. The range of decimal values for X in this representation is
2-f to 2i | |
2-f to (2i - 2-f) | |
0 to 2i | |
0 to (2i - 2-f ) |
Number of bits in fraction part → f-bits
Number of bits in integer part → (n – f) bits
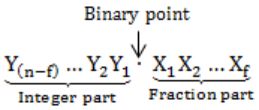
Minimum value:
000…0.000…0 = 0
Maximum value:
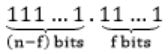
= (2 n-f - 1) + (1 - 2 -f
= (2n-f - 2 -f)
= (2i - 2 -f )
Question 8 |
Consider the C code fragment given below.
typedef struct node {
int data;
node* next;
} node;
void join(node* m, node* n) {
node* p = n;
while(p→next !=NULL) {
p = p→next;
}
p→next=m;
}
Assuming that m and n point to valid NULL-terminated linked lists, invocation of join will
append list m to the end of list n for all inputs. | |
either cause a null pointer dereference or append list m to the end of list n. | |
cause a null pointer dereference for all inputs. | |
append list n to the end of list m for all inputs. |
So have to consider both the cases.
⇾ 1. Lists are not null, invocation of JOIN will append list m to the end of list n.
m = 1, 2, 3
n = 4, 5, 6
After join, it becomes 4, 5, 6, 1, 2, 3, NULL.
⇾ 2. If lists are null, if the list n is empty, and itself NULL, then joining & referencing would obviously create a null pointer issue.
Hence, it may either cause a NULL pointer dereference or appends the list m to the end of list n.
Question 9 |
When two 8-bit numbers A7...A0 and B7...B0 in 2’s complement representation (with A0 and B0 as the least significant bits) are added using a ripple-carry adder, the sum bits obtained are S7...S0 and the carry bits are C7...C0. An overflow is said to have occurred if
the carry bit C7 is 1 | |
all the carry bits (C7,…,C0) are 1 | |
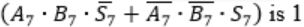 | |
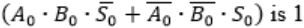 |
i.e., A7 = B7
⇾ Overflow can be detected by checking carry into the sign bits (Cin) and carry out of the sign bits (Cout).
⇾ Overflow occurs iff A7 = B7 and Cin ≠ Cout
These conditions are equivalent to
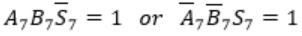
Consider
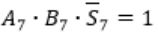
Here A7 = B7 = 1 and S7 = 0
This happens only if Cin = 0
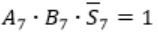
Carry out Cout=1 when
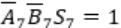
Similarly, in case of
Cin=1 and Cout will be 0.
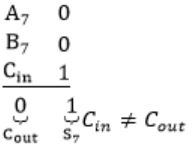
Question 10 |
S → abScT | abcT
T → bT | b
Which one of the following represents the language generated by the above grammar?
{(ab)n (cb)n│n ≥ 1} | |
{(ab)n cb(m1 ) cb(m2 )…cb(mn )│n,m1,m2,…,mn ≥ 1} | |
{(ab)n (cbm)n│m,n ≥ 1} | |
{(ab)n (cbn)m│m,n ≥ 1} |
S→ abScT | abcT, this production will generate equal number of “ab” and “c” and for every “abc” any number of b’s ( > 1) after “abc”.
For Ex:

Hence the language generated by the grammar is
L = {(ab)n cb(m1 ) cb(m2 )…cb(mn )│n,m1,m2,…,mn ≥ 1}
Question 11 |
Consider the C struct defined below:
struct data {
int marks [100];
char grade;
int cnumber;
};
struct data student;
The base address of student is available in register R1. The field student.grade can be accessed efficiently using
Post-increment addressing mode, (R1)+ | |
Pre-decrement addressing mode, -(R1) | |
Register direct addressing mode, R1 | |
Index addressing mode, X(R1), where X is an offset represented in 2’s complement 16-bit representation |
{
int marks[100];
char grade;
int cnumber;
}; struct data student
Base Address of student is available in R1.
So student.grade can be accessed efficiently by Relative Indexed Addressing Mode.
It is clearly mentioned X is the offset address to be summed with Base Address of R1.
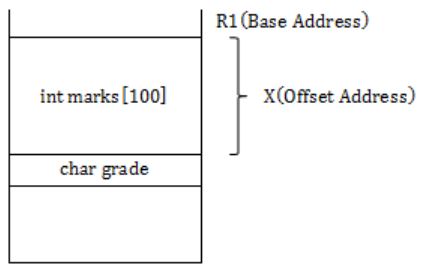
Hence Index Addressing mode X(R1), where X is an offset represented in 2’s complement 16-bit representation.
⇾ Relative, Base Indexed & all subtypes of Indirect addressing modes are used with Arrays.
Question 12 |
Consider the following intermediate program in three address code
p = a - b
q = p * c
p = u * v
q = p + q
Which of the following corresponds to a static single assignment form of the above code?
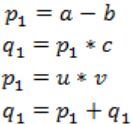 | |
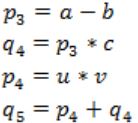 | |
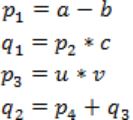 | |
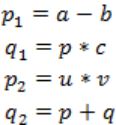 |
In Static Single Assignment form (SSA) each assignment to a variable should be specified with distinct names.
We use subscripts to distinguish each definition of variables.
In the given code segment, there are two assignments of the variable p
p = a-b
p = u*v
and two assignments of the variable q
q = p*c
q = p+q
So we use two variables p1, p2 for specifying distinct assignments of p and q1, q2 for each assignment of q.
Static Single Assignment form(SSA) of the given code segment is:
p1 = a-b
q1 = p1 * c
p2 = u * v
q2 = p2 + q1
Note:
As per options, given in GATE 2017 answer is B.
p3 = a - b
q4 = p3 * c
p4 = u * v
q5 = p4 + q4
Question 13 |
Consider the following C code:
#include <stdio.h>
int *assignval(int *x, int val) {
*x = val;
return x;
}
void main ( ) {
int *x = malloc(sizeof(int));
if(NULL == x) return;
x = assignval(x, 0);
if(x) {
x = (int *)malloc(size of(int));
if(NULL == x) return;
x = assignval(x, 10);
}
printf("%dn", *x);
free(x);
}
The code suffers from which one of the following problems:
compiler error as the return of malloc is not typecast approximately | |
compiler error because the comparison should be made as x==NULL and not as shown | |
compiles successfully but execution may result in dangling pointer | |
compiles successfully but execution may result in memory leak |
In C++, we need to perform type casting, but in C Implicit type casting is done automatically, so there is no compile time error, it prints10 as output.
Option B:
NULL means address 0, if (a == 0) or (0 == a) no problem, though we can neglect this, as it prints 10.
Option C:
x points to a valid memory location. Dangling Pointer means if it points to a memory location which is freed/ deleted.
int*ptr = (int*)malloc(sizeof(int));
free(ptr); //ptr becomes a dangling pointer
ptr = NULL; //Removing Dangling pointers condition
Option D:
x is assigned to some memory location
int*x = malloc(sizeof(int));
→ (int*)malloc(sizeof(int)) again assigns some other location to x, previous memory location is lost because no new reference to that location, resulting in Memory Leak.
Hence, Option D.
Question 14 |
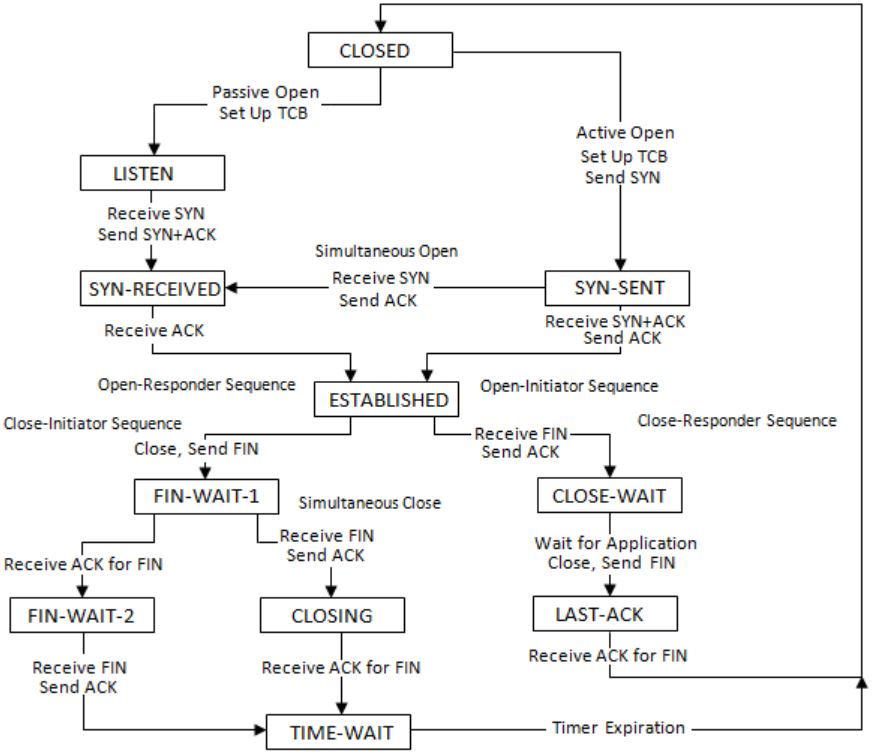
Consider a TCP client and a TCP server running on two different machines. After completing data transfer, the TCP client calls close to terminate the connection and a FIN segment is sent to the TCP server. Server-side TCP responds by sending an ACK, which is received by the client-side TCP. As per the TCP connection state diagram (RFC 793), in which state does the client-side TCP connection wait for the FIN from the server-side TCP?
LAST-ACK | |
TIME-WAIT | |
FIN-WAIT-1 | |
FIN-WAIT-2 |
i.e. waiting for the ACK for own FIN segment.
There are two possibilities here:
I. If Client receives ACK for its FIN then client will move to FIN-WAIT-2 and will wait for matching FIN from server side.
After receiving the FIN from server, client will send ACK and move to TIME-WAIT state.
II. Client has sent FIN segment but didn’t get ACK till the time.
Instead of ACK, client received FIN from server side.
Client will acknowledge this FIN and move to CLOSE state.
Here Client will wait for the ACK for its own FIN.
After receiving ACK, client will move to TIME-WAIT state.
Here we encounter First Case.
So, the solution is (D).
Refer this TCP state transition diagram:
Question 15 |
(I) S can launch a birthday attack to replace m with a fraudulent message.
(II) A third party attacker can launch a birthday attack to replace m with a fraudulent message.
(III) R can launch a birthday attack to replace m with a fraudulent message.
Which of the following are possible security violations?
(I) and (II) only | |
(I) only | |
(II) only | |
(II) and (III) only |
(I) Can the sender replace the message with a fraudulent message?
Yes, definitely because the sender will encrypt the message with its private key.
It can encrypt another message also with its private key.
(II) Can the third party send a fraudulent message?
No, because the third party doesn't know about the private key of the sender.
(III) Can receiver send the fraudulent message?
No, the receiver also doesn't know about the Private key of the sender.
So receiver also cannot send the fraudulent message.
Question 16 |
V → W
VW → X
Y → VX
Y → Z
Which of the following is irreducible equivalent for this set of functional dependencies?
V→W V→X Y→V Y→Z | |
V→W W→X Y→V Y→Z | |
V→W V→X Y→V Y→X Y→Z | |
V→W W→X Y→V Y→X Y→Z |
V → W, VW → X, Y → V, Y → X, Y→ Z
Step 2:
V → W, VW → X, Y → V, Y → X, Y→ Z
(V)+ = V ×
(VW)+ = VW ×
(Y)+ = YXZ
(Y)+ = YVW ×
(Y)+ = YVWX
Without Y → X, the closure of Y is deriving ‘X’ from the remaining attributes.
So, we can remove Y → X as its redundant.
Step 3:
V → W, VW → X, Y → V, Y → Z
(V)+ = VW, the closure of V is deriving W from the remaining FD’s.
So, W is redundant. We can remove it.
So, the final canonical form is
V→W, V→X, Y→V, Y→Z
⇾ So, option (A) is correct.
![GATE 2017 [Set-1]](https://solutionsadda.in/wp-content/uploads/2019/05/green-new-logo.png)