GATE 1999

Question 1
Suppose that the expectation of a random variable X is 5. Which of the following statements is true?
A
There is a sample point at which X has the value 5.
B
There is a sample point at which X has value greater than 5.
C
There is a sample point at which X has a value greater than or equal to 5.
D
None of the above
Engineering-MathematicsProbability
Question 1 Explanation: 
Expectation of discrete random variable
E(X) = x1P1 + x2P2 + ... + xnPn
In question, E(X) is given as 5.
E(X) = 5, 0≤Pi≤1
P1 + P2 + ... + Pn = 1 [Probability]
Therefore, E(X) = 5 is possible only if atleast one of the xi value is greater than 5.
Question 2
The number of binary relations on a set with n elements is:
A
n2
B
2n
C
2n (2)
D
None of the above
Engineering-MathematicsSets-And-Relation
Question 2 Explanation: 
In binary relation two elements are selected from a set. So total no. of pairs possible are
n×n = n2
Now, no. of binary relations possible is
2n2
Because each pair have two possibilities either chosen or not chosen.
Question 3

The  number  of  binary  strings  of  n  zeroes  and  k  ones  that  no  two  ones  are adjacent is

A
n-1Ck
B
nCk
C
nCk+1
D
None of the above
Engineering-MathematicsCombinatorics
Question 3 Explanation: 
Since there are n zeroes, so
XOXOXOXOXOXOX
n+1 gaps can be possible, where 1's can be placed so that no two one's are adjacent. So, no. of ways in which k 1's can be placed in n+1 gaps are,
n+1Ck
Question 4

Consider the regular expression (0 + 1) (0 + 1)…. N times. The minimum state finite  automation  that  recognizes  the  language  represented  by  this  regular expression contains

A
n states
B
n + 1 states
C
n + 2 states
D
None of the above
Theory-of-ComputationFinite-Automata
Question 4 Explanation: 
Let's draw both NFA and DFA and see which one requires less no. of state.
DFA:

So, DFA requires (n+2) state.
NFA:

So, NFA requires (n+1) state.
So, final answer will be,
min(n+1, n+2)
= n+1
Question 5

Context-free languages are closed under:

A
Union, intersection
B
Union, Kleene closure
C
Intersection, complement
D
Complement, Kleene closure
Theory-of-ComputationContext-Free-Language
Question 5 Explanation: 
Context free languages are not closed under Intersection and complementation.
By checking the options only option B is correct.
Question 6

Let LD be the set of all languages accepted by a PDA by final state and LE the set of all languages accepted by empty stack. Which of the following is true?

A
LD = LE
B
LD ⊃ LE
C
LE = LD
D
None of the above
Theory-of-ComputationPush-Down-Automata
Question 6 Explanation: 
For any PDA which can be accepted by final state, there is an equivalent PDA which can also be accepted by an empty stack and for any PDA which can be accepted by an empty stack, there is an equivalent PDA which can be accepted by final state.
Question 7
Which of the following expressions is not equivalent to
?
A
x NAND X
B
x NOR x
C
x NAND 1
D
x NOR 1
Digital-Logic-DesignLogic-Gates
Question 7 Explanation: 
Question 8
Which of the following functions implements the Karnaugh map shown below?
A
B
C
D
Digital-Logic-DesignK-Map
Question 8 Explanation: 

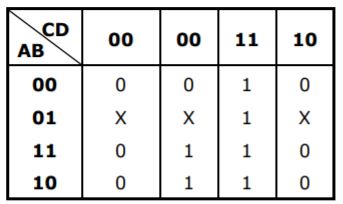
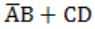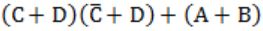⇒ CD+AD = D(A+C)
Question 9

Listed below are some operating system abstractions (in the left column) and the hardware components or mechanism (in the right column) that they are abstractions of. Which of the following matching of pairs is correct? 

    A. Thread                      1. Interrupt
    B. Virtual address space       2. Memory
    C. File system                 3. CPU
    D. Signal                      4. Disk
A
(A) – 2 (B) – 4 (C) – 3 (D) - 1
B
(A) – 1 (B) – 2 (C) – 3 (D) – 4
C
(A) – 3 (B) – 2 (C) – 4 (D) - 1
D
(A) – 4 (B) – 1 (C) – 2 (D) – 3
Operating-SystemsMatch-the-Following
Question 9 Explanation: 

⇒ Threads are handled by CPU.
⇒ Virtual address is a memory type.
⇒ File system is used to manage the disk.
⇒ Interrupt is a signal.
Question 10

Which of the following disk scheduling strategies is likely to give the best through put?

A
Farthest cylinder next
B
Nearest cylinder next
C
First come first served
D
Elevator algorithm
Operating-SystemsDisk-Scheduling
Question 10 Explanation: 
Farthest cylinder next - Longest job first
Nearest cylinder next - SSTF
First come first served - FCFS
Elevator - SCAN
SSTF always serves the request of nearest cylinder first. Due to which the necessary movement gets reduced.
Question 11

System calls are usually invoked by using

A
a software interrupt
B
polling
C
an indirect jump
D
a privileged instruction
Operating-SystemsSystem-Calls
Question 11 Explanation: 
Software interrupts are implementing device drivers (or) transitions between protected mode of operations, such as system calls.
Question 12

A sorting technique is called stable if

A
it takes O (nlog n) time
B
it maintains the relative order of occurrence of non-distinct elements
C
it uses divide and conquer paradigm
D
it takes O(n) space
Algorithms Sorting
Question 12 Explanation: 
Sorting techniques are said to be stable if it maintains the relative order of occurrence of non-distinct element.
Question 13

Suppose  we  want  to  arrange  the  n  numbers  stored  in any  array  such  that  all negative  values  occur  before  all  positive  ones. Minimum  number  of  exchanges required in the worst case is

A
n - 1
B
n
C
n + 1
D
None of the above
Algorithms Time-Complexity
Question 13 Explanation: 
Minimum no. of exchanges required in worst case will be when 1st half will contain all +ve nos and 2nd half will contain all -ve nos.
Now we will swap 1st no. with nth no. and then 2nd no. with (n-1)th no. and then 3rd no. with (n-2)th and so on. Like this we will have to do n/2 swaps in worst case.
Question 14

If one uses straight two-way merge sort algorithm to sort the following elements in ascending order: 

   20, 47, 15, 8, 9, 4, 40, 30, 12, 17

then the order of these elements after second pass of the algorithm is:

A
8, 9, 15, 20, 47, 4, 12, 17, 30, 40
B
8, 15, 20, 47, 4, 9, 30, 40, 12, 17
C
15, 20, 47, 4, 8, 9, 12, 30, 40, 17
D
4, 8, 9, 15, 20, 47, 12, 17, 30, 40
Algorithms Sorting
Question 14 Explanation: 
Question 15

The number of articulation points of the following graph is


A
0
B
1
C
2
D
3
Data-StructuresGraphs
Question 15 Explanation: 
Here, vertex 2, 3, 5 are the articulation points. By removing these vertices then the graph will be disconnected.
Total no. of articulation points = 3
Question 16

If n is a power of 2, then the minimum number of multiplications needed to compute a* is

A
log2 n
B
√n
C
n-1
D
n
Algorithms Time-Complexity
Question 16 Explanation: 

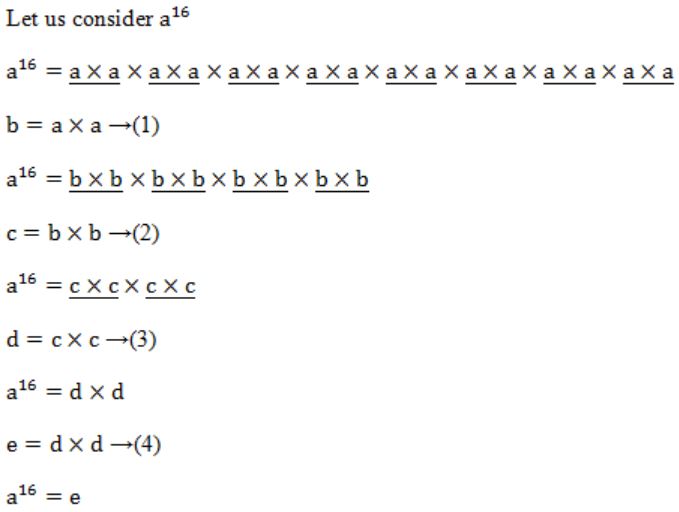
We require 4 multiplications to calculate a16 .....(I)
→ Like that 3 multiplications requires to calculate a8 .....(II)
I, II are satisfied with the option A.
Question 17

Which of the following is the most powerful parsing method?

A
LL (1)
B
Canonical LR
C
SLR
D
LALR
Compiler-DesignParsers
Question 17 Explanation: 
Canonical LR is most powerful.
LR > LALR > SLR
Question 18

Consider the join of a relation R with a relation S. If R has m tuples and S has n tuples then the maximum and minimum sizes of the join respectively are

A
m + n and 0
B
mn and 0
C
m + n and |m – n|
D
mn and m + n
Database-Management-SystemRelational-Algebra
Question 18 Explanation: 
For maximum:
Suppose there is no common attribute in R and S due to which natural join will act as cross product. So then in cross product total no. of tuples will be mn.
For minimum:
Suppose there is common attribute in R and S, but none of the row of R matches with rows of S then minimum no. of tuples will be 0.
There are 18 questions to complete.

Access quiz wise question and answers by becoming as a solutions adda PRO SUBSCRIBER with Ad-Free content

If you have registered and made your payment please contact solutionsadda.in@gmail.com to get access