GATE 2013
Question 1 |
A binary operation ⊕ on a set of integers is defined as x ⊕ y = x2 + y2. Which one of the following statements is TRUE about ⊕?
Commutative but not associative | |
Both commutative and associative | |
Associative but not commutative | |
Neither commutative nor associative |
A binary relation on a set S is called cumulative if a*b = b*a ∀ x,y∈S.
Associative property:
A binary relation on set is called associative if (a*b)*c = a*(b*c) ∀ x,y∈S.
Given x⊕y = x2 + y2 --------(1)
Replace x, y in (1)
y⊕x = y2 + x2 which is same as (1), so this is cumulative
(x⊕y)⊕z = (x2 + y2) ⊕ z
= (x2 + y2) + z2
= x2 + y2 + z2 + 2x2y2 ----------(2)
x⊕(y ⊕ z) = x ⊕ (y2 + z2)
= x2 + (y2 + z2)2
= x2 + y2 + z2 + 2y2z2 ----------- (3)
(2) & (3) are not same so this is not associative.
Question 2 |
Suppose p is the number of cars per minute passing through a certain road junction between 5 PM and 6 PM, and p has a Poisson distribution with mean 3. What is the probability of observing fewer than 3 cars during any given minute in this interval?
8/(2e3) | |
9/(2e3) | |
17/(2e3) | |
26/(2e3) |
P(x : λ) = (e-λ λx)/x! for x = 0,1,2….
‘λ’ is the average number (mean)
Given that mean = λ = 3
The probability of observing fewer than three cars is
P(zero car) + P(one car) + P(two cars)
= (e-3 30)/0!+(e-3 31)/1!+(e-3 32)/2!
= e-3+e-3∙3+(e-3)∙9)/2
= (17e-3<)/2
= 17/(2e3 )
Question 3 |
Which one of the following does NOT equal to
 | |
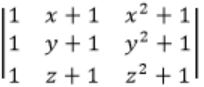 | |
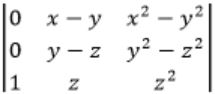 | |
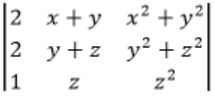 |
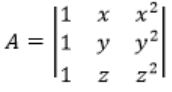
Try to derive options from the given matrix.
Observe that col 2 + col 3 will reuse x(x+1) term
C2 → C1 + C2
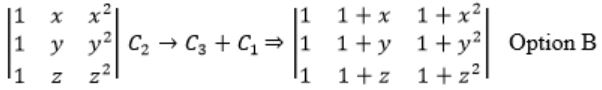
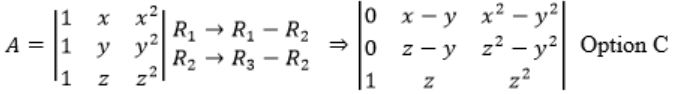
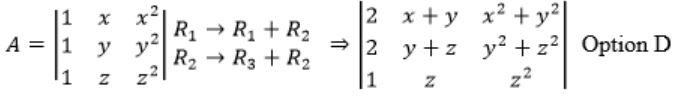
Question 4 |
The smallest integer that can be represented by an 8-bit number in 2’s complement form is
-256 | |
-128 | |
-127 | |
0 |
The smallest 8-bit 2’s complement number is 1000 0000.
MSB is 1. So it is a negative number.
To know the magnitude again take 2’s complement of 1000 0000.
1000 0000
0111 1111 ← 1’s complement
1000 0000 ← 2’s complement (1’s complement +1)
= 128
-128 is 1000 0000 in 2’s complement representation.
Question 5 |
In the following truth table, V = 1 if and only if the input is valid.
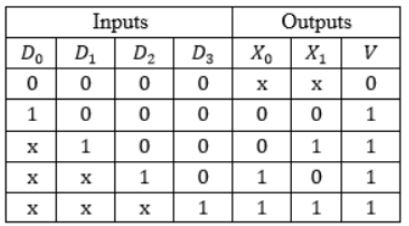
What function does the truth table represent?
Priority encoder | |
Decoder | |
Multiplexer | |
Demultiplexer |
Question 6 |
Which one of the following is the tightest upper bound that represents the number of swaps required to sort n numbers using selection sort?
O(log n) | |
O(n) | |
O(n log n) | |
O(n2) |
Selection sort time complexity O(n2) in terms of number of comparisons. Each of these scans requires one swap for n-1 elements (the final element is already in place).
Question 7 |
Which one of the following is the tightest upper bound that represents the time complexity of inserting an object into a binary search tree of n nodes?
O(1) | |
O(log n) | |
O(n) | |
O(n log n) |
Question 8 |
Consider the languages L1 = ϕ and L2 = {a}. Which one of the following represents L1L2* ∪ L1*?
{є} | |
ϕ | |
a* | |
{є,a} |
Rϕ = ϕR = ϕ
So L1 L2 * = ϕ
and L1 * = {ϕ}* = {ϵ}
So L1L2* ∪ L1* = {ϵ}
Question 9 |
What is the maximum number of reduce moves that can be taken by a bottom-up parser for a grammar with no epsilon- and unit-production (i.e., of type A → є and A → a) to parse a string with n tokens?
n/2 | |
n-1 | |
2n-1 | |
2n |
1) epsilon production
2) production of the form A → a
Consider the grammar:
S → Sa | a
If we were to derive the string “aaa” whose length is 3 then the number of reduce moves that would have been required are shown below:
S → Sa
→ Saa
→ aaa
This shows us that it has three reduce moves. The string length is 3 and the number of reduce moves is also 3. So presence of such kinds of production might give us the answer “n” for maximum number of reduce moves. But these productions are not allowed as per the question.
Also note that if a grammar does not have unit production then the maximum number of reduce moves can not exceed “n” where “n” denotes the length of the string.
3) No unit productions
Consider the grammar:
S → A
A → B
B → C
C → a
If we were to derive the string “a” whose length is 1 then the number of reduce moves that would have been required are shown below:
S → A
A → B
B → C
C → a
This shows us that it has four reduce moves. The string length is 1 and the number of reduce moves is 4. So presence of such kind of productions might give us the answer “n+1” or even more, for maximum number of reduce moves. But these productions are not allowed as per the question.
Now keeping in view the above points suppose we want to parse the string “abcd”. (n = 4) using bottom-up parsing where strings are parsed finding the rightmost derivation of a given string backwards. So here we are concentrating on deriving right most derivations only.
We can write the grammar which accepts this string which in accordance to the question, (i.e., with no epsilon- and unit-production (i.e., of type A → є and A → B) and no production of the form A → a) as follows:
S → aB
B → bC
C → cd
The Right Most Derivation for the above is:
S → aB (Reduction 3)
→ abC (Reduction 2)
→ abcd (Reduction 1)
We can see here the number of reductions present is 3.
We can get less number of reductions with some other grammar which also doesn’t produce unit or epsilon productions or production of the form A → a
S → abA
A → cd
The Right Most Derivation for the above is:
S → abA (Reduction 2)
→ abcd (Reduction 1)
Hence 2 reductions.
But we are interested in knowing the maximum number of reductions which comes from the 1st grammar. Hence total 3 reductions as maximum, which is (n – 1) as n = 4 here.
Question 10 |
A scheduling algorithm assigns priority proportional to the waiting time of a process. Every process starts with priority zero (the lowest priority). The scheduler re-evaluates the process priorities every T time units and decides the next process to schedule. Which one of the following is TRUE if the processes have no I/O operations and all arrive at time zero?
This algorithm is equivalent to the first-come-first-serve algorithm. | |
This algorithm is equivalent to the round-robin algorithm. | |
This algorithm is equivalent to the shortest-job-first algorithm. | |
This algorithm is equivalent to the shortest-remaining-time-first algorithm. |
Question 11 |
Match the problem domains in GROUP I with the solution technologies in GROUP II
GROUP I GROUP II (P) Service oriented computing (1) Interoperability (Q) Heterogeneous communicating systems (2) BPMN (R) Information representation (3) Publish-find-bind (S) Process description (4) XML
P-1, Q-2, R-3, S-4 | |
P-3, Q-4, R-2, S-1 | |
P-3, Q-1, R-4, S-2 | |
P-4, Q-3, R-2, S-1 |
Question 12 |
The transport layer protocols used for real time multimedia, file transfer, DNS and email, respectively are
TCP, UDP, UDP and TCP | |
UDP, TCP, TCP and UDP | |
UDP, TCP, UDP and TCP | |
TCP, UDP, TCP and UDP |
DNS runs over UDP protocol within port no-53.
Email needs, SMTP protocol which runs over TCP protocol within port no –25.
Question 13 |
Using public key cryptography, X adds a digital signature to message M, encrypts <M, σ>, and sends it to Y, where it is decrypted. Which one of the following sequences of keys is used for the operations?
Encryption: X’s private key followed by Y’s private key; Decryption: X’s public key followed by Y’s public key | |
Encryption: X’s private key followed by Y’s public key; Decryption: X’s public key followed by Y’s private key | |
Encryption: X’s public key followed by Y’s private key; Decryption: Y’s public key followed by X’s private key | |
Encryption: X’s private key followed by Y’s public key; Decryption: Y’s private key followed by X’s public key |

Encryption: Source has to encrypt with its private key for forming Digital signature for Authentication. Source has to encrypt the (M, σ) with Y’s public key to send it confidentially.
Decryption: Destination Y has to decrypt first with its private key, then decrypt using source public key.
Question 14 |
Assume that source S and destination D are connected through two intermediate routers labeled R. Determine how many times each packet has to visit the network layer and the data link layer during a transmission from S to D.
Network layer – 4 times and Data link layer – 4 times | |
Network layer – 4 times and Data link layer – 3 times | |
Network layer – 4 times and Data link layer – 6 times | |
Network layer – 2 times and Data link layer – 6 times |
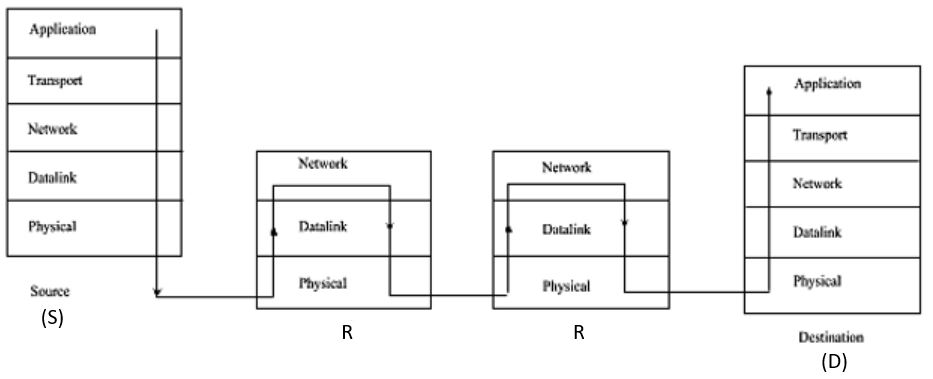
From above given diagram, its early visible that packet will visit network layer 4 times, once at each node [S, R, R, D] and packet will visit Data Link layer 6 times. One time at S and one time at D, then two times for each intermediate router R as data link layer is used for link to link communication.
One at packet reaches R and goes up from physical –DL-Network and second time when packet coming out of router in order Network –DL-Physical.
Question 15 |
An index is clustered, if
it is on a set of fields that form a candidate key. | |
it is on a set of fields that include the primary key. | |
the data records of the file are organized in the same order as the data entries of the index. | |
the data records of the file are organized not in the same order as the data entries of the index. |
Basically, Indexed column is used to sort the rows of table. Whole data record of file is sorted using index so the correct option is (C).
Question 16 |
Three concurrent processes X, Y, and Z execute three different code segments that access and update certain shared variables. Process X executes the P operation (i.e., wait) on semaphores a, b and c; process Y executes the P operation on semaphores b, c and d; process Z executes the P operation on semaphores c, d, and a before entering the respective code segments. After completing the execution of its code segment, each process invokes the V operation (i.e., signal) on its three semaphores. All semaphores are binary semaphores initialized to one. Which one of the following represents a deadlock-free order of invoking the P operations by the processes?
X: P(a)P(b)P(c) Y: P(b)P(c)P(d) Z: P(c)P(d)P(a) | |
X: P(b)P(a)P(c) Y: P(b)P(c)P(d) Z: P(a)P(c)P(d) | |
X: P(b)P(a)P(c) Y: P(c)P(b)P(d) Z: P(a)P(c)P(d) | |
X: P(a)P(b)P(c) Y: P(c)P(b)P(d) Z: P(c)P(d)P(a) |

