GATE 2017 [Set-2]
Question 1 |
The representation of the value of a 16-bit unsigned integer X in hexadecimal number system is BCA9. The representation of the value of X in octal number system is
136251 | |
736251 | |
571247 | |
136252 |
Each hexadecimal digit is equal to a 4-bit binary number. So convert
X = (BCA9)16 to binary

Divide the binary data into groups 3 bits each because each octal digit is represented by 3-bit binary number.
X = (001 011 110 010 101 001)2
Note: Two zeroes added at host significant position to make number bits of a multiple of 3 (16 + 2 = 18)
X = (136251)8
Question 2 |
Match the following:
P→(ii), Q→(iv), R→(i), S→(iii) | |
P→(ii), Q→(i), R→(iv), S→(iii) | |
P→(ii), Q→(iv), R→(iii), S→(i) | |
P→(iii), Q→(iv), R→(i), S→(ii) |
⇾ A variable located in Data Section of memory

P→(ii), Q→(iv), R→(i), S→(iii)
Question 3 |
Match the algorithms with their time complexities:
Algorithm Time complexity (P) Towers of Hanoi with n disks (i) Θ(n2) (Q) Binary search given n stored numbers (ii) Θ(n log n) (R) Heap sort given n numbers at the worst case (iii) Θ(2n) (S) Addition of two n×n matrices (iv) Θ(log n)
P→(iii), Q→(iv), R→(i), S→(ii) | |
P→(iv), Q→(iii), R→(i), S→(ii) | |
P→(iii), Q→(iv), R→(ii), S→(i) | |
P→(iv), Q→(iii), R→(ii), S→(i) |
→ Tower of Hanoi with n disks takes θ(2n) time
It is a mathematical game or puzzle.
It consists of three rods and a number of disks of different sizes, which can slide onto any rod.
The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack.
3. No disk may be placed on top of a smaller disk.
With 3 disks, the puzzle can be solved in 7 moves.
The minimal number of moves required to solve a Tower of Hanoi puzzle is 2n-1, where n is the number of disks.
→ Binary Search given n sorted numbers takes Ɵ(log2 n)
→ Heap sort given n numbers of the worst case takes Ɵ(n log n)
→ Addition of two n×n matrices takes Ɵ(n2)
Question 4 |
Let L1, L2 be any two context-free languages and R be any regular language. Then which of the following is/are CORRECT?

I, II and IV only | |
I and III only | |
II and IV only | |
I only |
CFL is not closed under complementation.
So L1 compliment may or may not be CFL. Hence
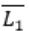 is Context free, is a false statement.
is Context free, is a false statement.L1 – R means
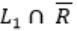 and Regular language is closed under compliment, so
and Regular language is closed under compliment, so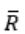 is also a regular language, so we have now L1 ∩ R .
is also a regular language, so we have now L1 ∩ R .Regular language is closed with intersection with any language, i.e. L∩R is same type as L.
So L1∩R is context free.
CFL is not closed under INTERSECTION, so L1 ∩ L2 may or may not be CFL and hence IVth is false.
Question 5 |
Match the following according to input (from the left column) to the compiler phase (in the right column) that processes it:
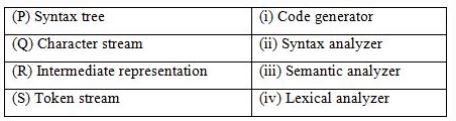
P→(ii), Q→(iii), R→(iv), S→(i) | |
P→(ii), Q→(i), R→(iii), S→(iv) | |
P→(iii), Q→(iv), R→(i), S→(ii) | |
P→(i), Q→(iv), R→(ii), S→(iii) |
Token stream is forwarded as input to Syntax analyzer which produces syntax tree as output. So, S → (ii).
Syntax tree is the input for the semantic analyzer, So P → (iii).
Intermediate representation is input for Code generator. So R → (i).
Question 6 |
Which of the following statements about parser is/are CORRECT?
I. Canonical LR is more powerful than SLR.
II. SLR is more powerful than LALR.
III. SLR is more powerful than Canonical LR.
I only | |
II only | |
III only | |
II and III only |
The power in increasing order is:
LR(0) < SLR < LALR < CLR
Hence only I is true.
Question 7 |
Which of the following is/are shared by all the threads in a process?
I. Program counter
II. Stack
III. Address space
IV. Registers
I and II only | |
III only | |
IV only | |
III and IV only |
A process, in the simplest terms, is an executing program.
One or more threads run in the context of the process.
A thread is the basic unit to which the operating system allocates processor time.
A thread can execute any part of the process code, including parts currently being executed by another thread.
Each thread has its own stack, register and PC.
So here address space that is shared by all thread for a single process.
Question 8 |
In a file allocation system, which of the following allocation scheme(s) can be used if no external fragmentation is allowed?
I. Contiguous
II. Linked
III. Indexed
I and III only | |
II only | |
III only | |
II and III only |
Advantage:
i) Both sequential and direct access is possible.
ii) Extremely fast.
Disadvantage:
i) Suffers from both internal and external fragmentation.
ii) Increasing file size is difficult, because it depends on the availability of contiguous memory at a particular instance.
→ Linked list allocation:
Advantage:
i) Flexible in terms of size.
ii) Does not suffers from external fragmentation.
Disadvantage:
i) Allocation is slower.
ii) Does not support random or direct access.
iii) Pointers require some extra overhead.
→ Indexed allocation:
Advantage:
i) Support direct access, so provides fast access to the file blocks.
ii) No external fragmentation.
Disadvantage:
i) The pointer overhead for indexed allocation is greater than linked allocation.
ii) Inefficient in terms of memory utilization.
Question 9 |
Consider the following statements about the routing protocols, Routing Information Protocol (RIP) and Open Shortest Path First (OSPF) in an IPv4 network.
-
- I: RIP uses distance vector routing
-
- II: RIP packets are sent using UDP
-
- III: OSPF packets are sent using TCP
- IV: OSPF operation is based on link-state routing
Which of the statements above are CORRECT?
I and IV only | |
I, II and III only | |
I, II and IV only | |
II, III and IV only |
RIP is one of the oldest DVR protocol which employ the hop count as a routing metric.
II: RIP packets are sent using UDP. “TRUE”
RIP uses the UDP as its transport protocol, and is assigned the reserved port no 520.
III: OSPF packets are sent using TCP. “FASLE”
OSPF encapsulates its data directly into IP Packets and does not use either TCP or UDP.
IV: OSPF operation is based on link state routing. “TRUE”
OSPF is a routing protocol which uses link state routing (LSR) and works within a single autonomous system.
Hence correct is answer “C”.
Question 10 |
If f(x) = Rsin(πx/2) + S, f'(1/2) = √2 and , then the constants R and S are, respectively.
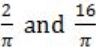 | |
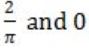 | |
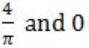 | |
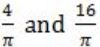 |
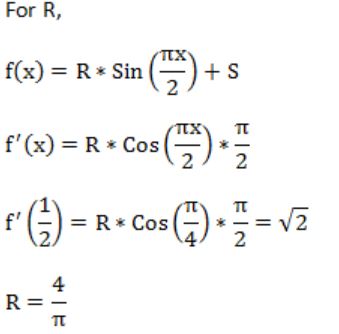
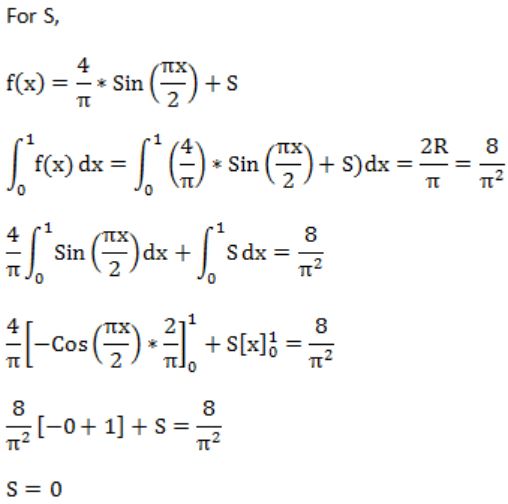
Question 11 |
Let p, q, r denote the statements “It is raining”, “It is cold”, and “It is pleasant”, respectively. Then the statement “It is not raining and it is pleasant, and it is not pleasant only if it is raining and it is cold” is represented by
(¬p ∧ r) ∧ (¬r → (p ∧ q)) | |
(¬p ∧ r) ∧ ((p ∧ q) → ¬r) | |
(¬p ∧ r) ∨ ((p ∧ q) → ¬r) | |
(¬p ∧ r) ∨ (r → (p ∧ q)) |
q: It is cold
r: It is pleasant
“If it is not raining and it is pleasant, and it is not pleasant only if it is raining and it is cold.”
We can divide the statement into two parts with “Conjunction”.
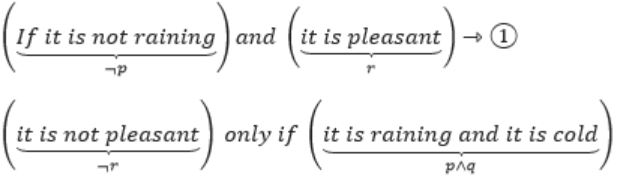
i.e., ¬r→(p∧q) ⇾(2)
From (1) & (2), the given statement can be represented as
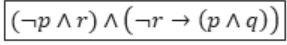
Question 12 |
Given the following binary number in 32-bit (single precision) IEEE-754 format:
The decimal value closest to this floating-point number is
1.45 × 101 | |
1.45 × 10-1 | |
2.27 × 10-1 | |
2.27 × 101 |

For single-precision floating-point representation decimal value is equal to (-1)5 × 1.M × 2(E-127)
S = 0
E = (01111100)2 = (124).
So E – 127 = - 3
1.M = 1.11011010…0
= 20 + 2(-1) + 2(-1) + 2(-4) + 2(-5) + 2(-7)
= 1+0.5+0.25+0.06+0.03+0.007
≈ 1.847
(-1)5 × 1.M × 2(E-127)
= -10 × 1.847 × 2-3
≈ 0.231
≈ 2.3 × 10-1
Question 13 |
I. Next pointer of front node points to the rear node.
II. Next pointer of rear node points to the front node.
I only | |
II only | |
Both I and II | |
Neither I nor II |
2. Next pointer of rear points to the front node.
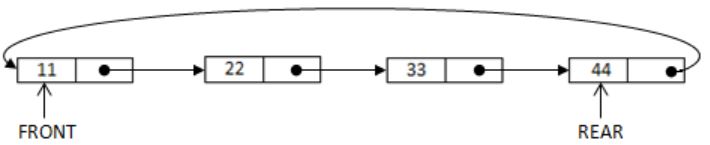
So if we consider circular linked list the next of 44 is 11.
If you place pointer on next of front node (11) then to reach 44 (last node), we have to traverse the entire list.
For delete O(1), for insert O(n).
It is clearly known that next pointer of rear node points to the front node.
Hence, only II is true.
Question 14 |
Consider the following function implemented in C:
void printxy (int x, int y) {
int *ptr;
x = 0;
ptr = &x;
y = *ptr;
*ptr = 1;
printf("%d,%d",x,y);
}
The output of invoking printxy(1, 1) is
0, 0 | |
0, 1 | |
1, 0 | |
1, 1 |
{
int *ptr;
x = 0;
ptr = &x;
y = *ptr;
*ptr = 1;
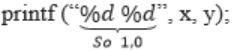
}
printxy (1, 1)
Question 15 |
The Breadth First Search (BFS) algorithm has been implemented using the queue data structure. Which one of the following is a possible order of visiting the nodes in the graph below?
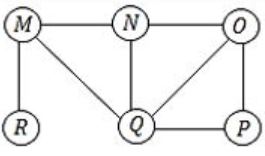
MNOPQR | |
NQMPOR | |
QMNROP | |
POQNMR |
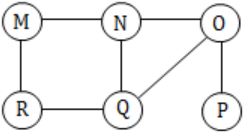
(Do it by option Elimination)
(a) MNOPQR – MNO is not the proper order R must come in between.
(b) NQMPOR – QMP is not the order O is the child of N.
(C) QMNROP – M is not the child of Q, so QMN is false.
(D) POQNMR – P → OQ → NMR is the correct sequence. Hence Option (D).
Question 16 |
Identify the language generated by the following grammar, where S is the start variable.
S → XY
X → aX|a
Y → aYb|ϵ
{am bn │ m ≥ n, n > 0} | |
{am bn │ m ≥ n, n ≥ 0} | |
{am bn │ m > n, n ≥ 0} | |
{am bn │ m > n, n > 0} |
So the production S→XY can generate any number of a’s (≥1) in the beginning (due to X) and then Y will generate equal number of a’s and b’s.
So, the number of a’s will always be greater than number of b’s and number of b’s must be greater than or equal to 0 (as Y → ϵ, so number of b’s can be zero also).
Hence the language is {am bn│m>n,n≥0}.
![GATE 2017 [Set-2]](https://solutionsadda.in/wp-content/uploads/2019/05/green-new-logo.png)
